ufjobs.blogg.se

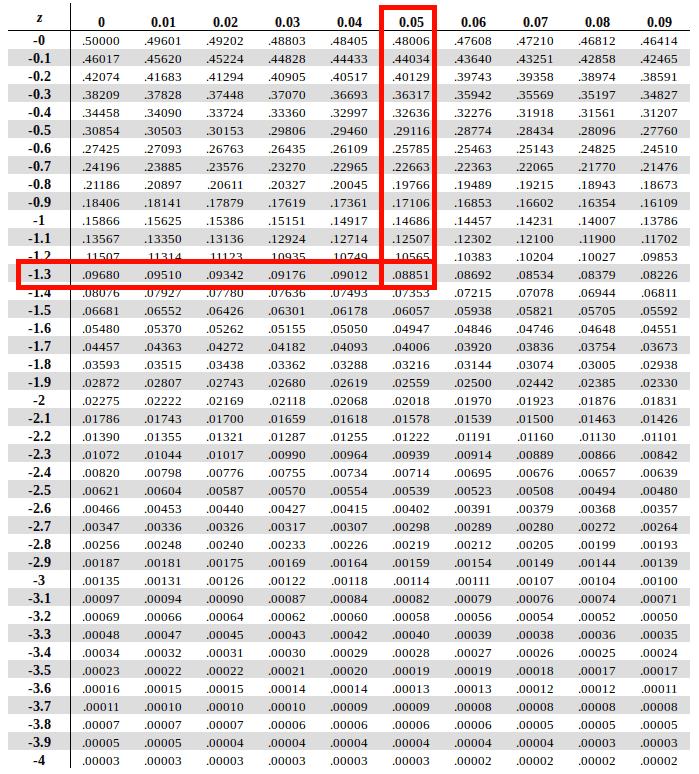
Now 𝑍 ∼ 𝑁  0, 1   follows the standard normal distribution and In order to find the unknown mean 𝜇, we code 𝑋 by the change of variables 𝑋 ↦ 𝑍 = 𝑋 − 𝜇 𝜎, where the standard deviation is

5 6 % into a probability, we divide byġ00, so we have 𝑃 ( 𝑋 < 4 7 ) = 0. To convert the population percentage of 1 0. We have a normal random variable 𝑋 ∼ 𝑁  𝜇, 1 2   with unknown mean. Of the flowers are shorter than 47 cm, determine 𝜇. The heights of a sample of flowers are normally distributed with mean 𝜇 and standard deviation 12 cm. Let us try applying these techniques in a real-life context to find an unknown mean.Įxample 5: Determining the Mean of a Normal Distribution in a Real-Life Context Thus, rounding to one decimal place, we have 𝜎 = 1. To find the value of 𝑎, we can substitute back into 𝑎 − 3. We can now eliminate 𝑎 by subtracting the second equation from the first:Ģ 𝑎 − 3. Then, we multiply the second of these by 2: This yields the pair of simultaneous equationsĢ 𝑎 − 3. Example 4: Finding Unknown Quantities in Normal DistributionsĬonsider the random variable 𝑋 ∼ 𝑁  3.